Supponiamo di sparare un proiettile orizzontalmente. Scegliamo l’asse x orizzontale e l’asse y verticale e diretto verso il basso.
Possiamo scomporre la velocità del proiettile in una componente orizzontale (xV) e in una verticale (yV) e considerare il suo moto come la sovrapposizione di due moti indipendenti: uno lungo x e l’altro lungo y.
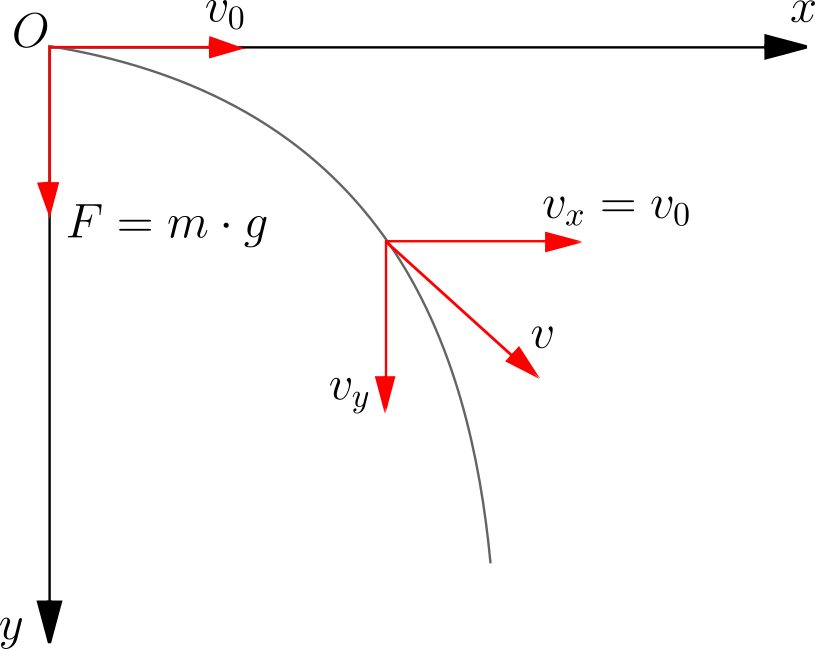
Il proiettile lascia la canna all’istante t = 0 con una velocità iniziale v0 e da questo momento in poi agisce su esso solo la forza peso diretta sull’asse y e nessuna forza diretta sull’asse x. Quindi ad ogni istante t > 0 :
Esaminiamo il caso più generale: il moto di un proiettile con velocità iniziale v0 formante un angolo ϑ con la direzione orizzontale.
Scomponiamo la velocità in due componenti e studiamo il moto nelle due direzioni.
La seguente equazione della traiettoria rappresenta geometricamente una parabola:
L’ordinata di A è l’altezza massima (h) raggiunta dal proiettile che si può calcolare osservando yV che si annulla in A per poi cambiare segno.