Disegniamo il pendolo per capire quali forze agiscono su di esso:
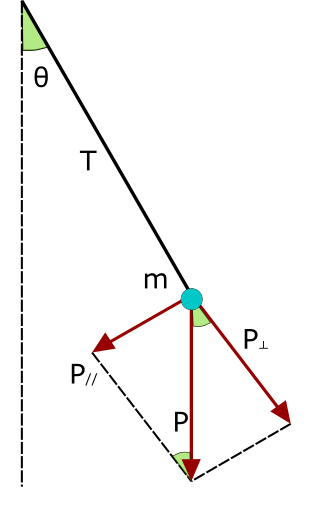
Man mano che oscilla il punto di massa m si allontana dall’origine di una distanza x che rappresenta l’ampiezza del moto di oscillazione. Θ è definito come l’angolo che la fune crea con la verticale.
Sul punto agiscono due sole forze: la forza peso P diretta verso il basso e la tensione T della fune.
La forza la scomporremo nelle sue due componenti, quella parallela e quella perpendicolare.
Se volessimo trovare l’accelerazione che agisce sul punto di massa m, dovremo applicare il secondo principio della dinamica.
Sull’asse orizzontale compare solamente la componente parallela della forza peso:
Logicamente g è l’accelerazione di gravità. Considerando che si forma un triangolo rettangolo con ipotenusa la fune di lunghezza L e per cateto orizzontale la distanza x possiamo scrivere la relazione:
Allora possiamo riscrivere la componente parallela della forza peso come:
Poiché la componente P// punta verso il lato negativo dell’asse x, allora scriviamo il secondo principio della dinamica come:
Semplificando il tutto e con una formula inversa otterremo: